La teoria di Bohr Sommerfeld riuscì a spiegare l’origine delle righe spettrali dell’atomo di idrogeno che contiene solo un elettrone, ma purtroppo non era applicabile agli altri tipi di atomi con un numero di elettroni superiore a quello dell’idrogeno.. Non solo, ma un esperimento del fisico Heisnberg dimostrò che era impossibile misurare con certezza il momento dell’elettrone e contemporaneamente la sua posizione così come la teoria di Bohr e Sommerfeld sosteneva.
Sappiamo che per conoscere una grandezza fisica in campo macroscopico si adopera in genere uno strumento adatto che fornisce poi il risultato della misura della grandezza fisica cercato. Se, invece, si vuole ottenere il valore di una grandezza fisica in campo microscopico, l’utilizzazione di uno strumento per la misura produce una perturbazione del sistema stesso e molto spesso è notevole.
Heisnberg immaginò di usare un microscopio per valutare la quantità di moto cioè l’ energia di un elettrone in movimento.Ovviamente, per poter effettuare la misura, suppose che l’elettrone fosse fermo e si trovasse nel campo visivo del microscopio e per farlo muovere si potesse utilizzare una particella luminosa, il fotone, con lunghezza d’onda λ. Era evidente che l’uso di un fotone con λ grande, faceva uscire l’elettrone dal campo visivo che dipendeva dal rapporto λ/ 2 sen α deve α è l’angolo dell’obiettivo
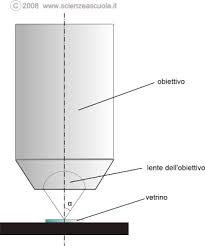
E’ chiaro che l’uso di una radiazione con un gran valore di λ causa,nell’urto, l’uscita dell’elettrone dal campo del microscopio impedendo la misura della velocità e quindi della quantità di moto. Si potrebbe risolvere il problema con l’uso di una λ piccolissima, ma purtroppo anche in questo caso si verifica un altro fenomeno chiamato EFFETTO COMPTON.
E’ noto infatti che se un fotone, che possiede una quantità di moto pari ad h ν / c ( h è la costante di Plank e ν la frequenza della radiazione (1/λ) e c la velocità della luce) , colpisce un elettrone inizialmente fermo, la sua quantità di moto subirà un a variazione da h ν/c ad h ν‘ /c. L’elettrone colpito si muoverà a sua volta con un’energia cinetica E= ½mv² ed una quantità di moto mv (massa per velocità dove la massa è la massa in movimento cioè m = mο / ( 1- V²/C²)½)
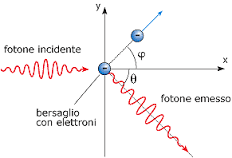
dopo l’urto la quantità di moto deve essere conservata per cui
h ν = h ν‘ +½ mV²
h ν /c = h ν‘/c cos θ + mv cos φ
dove h ν‘/c cos θ è la componente su x della quantità di moto del fotone.
mv cos φ è la componente sull’asse x della quantità di moto dell’elettrone
h ν‘/c cos θ = mv sen φ
si deduce che la quantità di moto del fotone dopo l’urto, è
P× = h ν /c – h ν‘/c cos θ P× = h/c x (ν-ν‘) cos θ
ricordando che
C/ = λ ν/C = 1/λ quindi Px = h/λ (1 – cos θ)
Affinchè il microscopio capti la luce diffusa, è necessario che l’angolo θ dopo l’urto sia compreso nel campo dell’obiettivo cioè tra 90- φ e 90 + φ . Quindi non vi è la possibilità di valutare il momento Px esattamente ma solo nei limiti definiti da 90- φ e 90 + φ . Ma
cos(90- φ) = sen φ e
cos(90+ φ) = sen φ
essendo Px = h/λ (1 – cos θ) e Px = h/λ (1 + cos θ)
Δpx = h/λ sen φ
Poichè il potere di risoluzione della lente del microscopio nella valutazione della posizione è limitato da
λ / sen φ si ha Δx ≅ λ / sen φ
pertanto
Δpx x Δx ≅ h/λ sen φ x λ / sen φ
Δpx x Δx ≅ h
questa conclusione ci dice che il prodotto tra queste incertezze è all’incirca pari ad h.
Possiamo concludere dicendo che se si cerca l’accuratezza nella misura della posizione, diminuisce contemporaneamente l’accuratezza nella misura del momento dell’elettrone e viceversa.
L’espressione matematica ricavata sopra è nota come PRINCIPIO DI INDETERMINATEZZA di Heisenberg.
E’ proprio questo il motivo per cui la teoria di Bohr è stata completamente abbandonata in quanto essa ammetteva la possibilità di una misura esatta contemporanea del momento e della posizione dell’elettrone, mentre, come ha ammesso Heisenberg, il principio di indeterminatezza è un principio generale della Natura.
Lascia un commento