1- In una reazione esotermica un sistema cede al suo intorno 8,243 J. Durante la reazione si formano dei gas che sollevano un pistone compiendo un lavoro di 4,184J. Calcolare ΔE.

Soluzione

Il calore viene ceduto dal sistema al suo intorno ed è quindi negativo:

q = – 8,243 J

il lavoro viene compiuto dal sistema sul suo intorno ed è quindi positivo:

w=L= 4,184J

La variazione di energia interna è:

ΔE = q – w = – 8,243 – 4,184 = —12,427J

2- La combustione di una mole di glucosio (C₆H₁₂0₆) alla pressione costante di 1,0 atm e alla temperatura di 20,0°C porta allo sviluppo di 673 kcal. Calcolare ΔE per questo processo.

Soluzione

Per combustione totale si intende l’ossidazione del glucosio con trasfor­mazione di tutto il carbonio in CO₂ e di tutto l’idrogeno in 14₂0. La com­bustione totale del glucosio può essere rappresentata mediante l’equazione chimica:

C₆H₁₂0₆ + 6O2 → 6CO₂ + 6H₂0

I dati del problema forniscono, per tale reazione, il valore di q:

q = – 673 kcal

il segno è negativo in quanto il calore viene ceduto dal sistema all’intorno. Per ricavare ΔE dalla dobbiamo ancora calcolare w. Dato che la rea­zione avviene a pressione costante possiamo scrivere:

w = PΔV    dove P = 1,0 atm.

Osservando la reazione di combustione totale, notiamo come tra i reagenti compaiano un solido (il glucosio) e un gas (l’ossigeno) mentre tra i prodotti della reazione abbiamo un gas (diossido di carbonio) un liquido (acqua). Dato che il volume occupato dai solidi e dai liquidi è piccolo rispetto al volume occupato dai gas, a parità di quantità di mat possiamo assumere che le variazioni di volume del sistema si identifi con le variazioni di volume della fase gassosa. Nel caso che stiamo nando, tuttavia, nel passare dai reagenti ai prodotti non si ha variazione numero

di moli di gas in quanto a 6 moli di ossigeno tra i reagenti e spondono 6 moli di CO₂ tra i prodotti. Per il sistema risulta quindi:

ΔV=0

W = O

ΔE = q = – 673 kcal

3- La decomposizione termica del carbonato di calcio (CaCO₃) porta alla formazione di ossido di calcio (CaO) e di diossido di carbonio (CO₂). Per comporre una mole di CaCO₃ a 25°C e 1 atmosfera occorrono 1,78 x J. Calcolare iE per la decomposizione di 1,00 g di CaCO₃.

Soluzione

Scriviamo la reazione di decomposizione termica del carbonato di cal CaCO₃ ^—4 CaO + CO₂

Calcoliamo a quante moli di CaCO₃ corrispondono 1,00 g sapendo la massa molecolare di CaCO₃ è 100,09 u:

1,00 g/ 100,09 g/mol = 9,99 x 10 ^-3 mol

Se la decomposizione di una mole di CaCO₃ richiede 1,78 x 10⁵ J, la composizione di

9,99x 10^-3 moli richiede:

(1,78 x 10⁵ J/mol) x  (9,99x 10^-3   mol) = 1,78 x 10³J

La decomposizione del carbonato di calcio comporta la formazione di un  solido (CaO) e di un gas (CO₂). La presenza di un gas tra i prodotti implica  un aumento del volume del sistema e la variazione di volume, per ogni mole di CaCO₃ che si decompone, è pari a:

ΔV= Δn RT / P = 1,0 mol   x 8,314 J/(mol x K) x 298 K/ 1 atm  = 2,48 x 10³ J/atm

dove R è espresso i J/mol x k.

La decomposizione di 9,99 x 10^-3 moli di CaCO₃ comporta  una variazione di volume pari a:

(2,48 x 10³) x (9,99 x 10^-3) = 24,8 J/atm

Il lavoro corrispondente è:

w =L=  PΔV 1,00 atm X 24,8 J/atm = 24,8 J

La variazione dell’energia interna è:

ΔE = q -w = 1,78 x 10³ —24,8 = 1,76 x  10³J

4-Sapendo che per la combustione del glucosio (C₆H₁₂0₆) ΔE = —2816 kJ/mol e che per la combustione dell’acido stearico (C₁₈H₃₆O₂) ΔE = —11326 kJ/mol, calcolare i valori di ΔΗ per la combustione del glucosio e dell’acido stearico alla temperatura di 293,2 K e alla pressione di un’atmosfera.

Soluzione

Scriviamo le reazioni di combustione del glucosio e dell’acido stearico:

C₆H₁₂O₆ + 6O₂ → 6CO₂ + 6H₂O
C₁₈H₃₆O₂ +26O₂ → 18CO₂ + 18H₂O

Sappiamo che per quelle reazioni per le quali non si ha variazione di volume nel passare dai reagenti ai prodottiΔH = ΔE. Dato che nella combustione del glucosio il numero di moli di gas reagenti è uguale al numero di moli di gas prodotti, AV = O. Ne deriva immediata­mente che per la combustione del glucosio:

AH = ΔE  = – 2816 kJ

Nella combustione dell’acido stearico si verifica invece una diminuzione del volume del sistema in quanto a 26 moli di gas reagenti corrispondono 18 moli di gas prodotti. La combustione di una mole di acido stearico comporta quindi una diminuzione di volume del sistema pari a:

ΔV = Δn x  RT / P   = (18-26) mol X 8,3143 x 10^-3 kJ/(mol x K) x  293,2 K /  1,0 atm

ΔV = 19,50 kJ/atm

avendo posto R = 8,3143  x 10^-3 kJ/(mol x K). La variazione di entalpia è:

ΔH = ΔE + PΔV= —11326 kJ + 1,000  atm x (-19,50) kJ/atm = —11346kJ

5- Noto il calore specifico  di H2O liquida Cp _H2Ol = 1,00 cal /g °C, calcolare:

     a) il calore specifico molare di H2O liquida;

b) la quantità di calore in calorie ed in Jaule necessaria per portare 20 moli di H2O dalla temperatura di 20°C alla temperatura di 80°C

c) la variazione di energia interna del sistema.

soluzione

Si deve eseguire la seguente trasformazione:

20 molH2O_(l)(20 °C) → 20 mol H2O _(l)  (80 °C)

Noto il Cp dell’acqua e la massa di 1 mole d’acqua (18,0 g / mol ) il calore specifico  molare Cp risulta:

Cp = 1,00(cal /g °C)  x 18,0(g / mol) = 18,0 cal  /mol °C

Il calore necessario per la trasformazione è dato da:

Q =  n x  Cp Δt

Sostituendo ,si ha:

Q = 20,0 (mol) x 18,0 (cal/ mol °C) x 60,0 (°C) = 21,6 x 10³ cal

Poichè 1 cal = 4,184 J,la quantità di calore espressa in J è :

Q = 21,6 x 10³ (cal) x 4,184 (J /cal) = 90,4 x 10³ J

La trasformazione avviene senza apprezzabile variazione di volume perciò  L = P • ΔV = 0 e poichè ΔΕ =Q – L , risulta  ΔΕ = 0

Al sistema vengono forniti 90,4 x 10³ J,perciò,

Q= ΔΕ = 90,4 x 10³ J/ 1000 (J kJ^–1) = 90,4  kJ

L’energia interna del sistema aumenta quindi di 90,4 kJ.

6-  Una quantità di calore pari a 10,0 cal viene fornita  a. 4,00 g di H2O,Cu ed Ag rispettivamente, che inizialmente si trovano tutti alla temperatura di 20 °C .
Calcolare la temperatura finale dei tre sistemi. Calcolare inoltre la variazione di energia interna di ciascun sistema. Cp H2O_{( l )} = 1,0 cal/g °C    Cp_Cu = 0,0921  cal/g °C  Cp_Ag = 0,558  cal/g °C 

soluzione

Le temperature  finali  si ricavano da:

Q(cal) = m(g) . c(cal /g °C) • (t_finale  – t i_niziale ) °C

Sistema H₂O:

10,0(cal) = 4,00(g) x 1,00(cal /g °C ) x [t fin – 20,0(°C)]

t_finale = 20 + 10/4,00 x 1,00 = 22,5 °C

Sistema Cu:

t_finale = 20,0  +10/ 4,00 x 0,0921 =    47,1 °C

Sistema Ag:

t_finale   = 20,0 +10/4,00 x 0,0559 = 64,8 °C

Per ciascuno dei tre sistemi: ΔΕ =Q – L.

Durante  le trasformazioni non viene scambiato lavoro,quindi:

L=0     e   ΔE=Q= 10,0 cal

La variazione d’energia interna per ciascun sistema è uguale a 10,0 cal.

L’energia fornita viene utilizzata  esclusivamente per aumentare la temperatura dei sistemi, cioè per aumentare l’energia cinetica delle particelle.

7-  10 g di Zn reagiscono con H2₂SO4 alla pressione costante di 1 atm e alla temperatura costante di 25 °C, secondo la reazione:

Zn₍S₎ + H2SO4   —-> H2(g) + ZnSO4 (aq)

cedendo all’ambiente 5200 cal.

Calcolare la variazione di energia interna del sistema ammettendo che il lavoro compiuto dallo stesso sull’ambiente sia solo di tipo meccanico.

soluzione

La variazione di energia interna è data dalla relazione:
U= Q – W oppure E = Q – L

Nell’ipotesi che W sia solo lavoro meccanico e tenendo presente che la pressione è costante, possiamo scrivere:

W= P(V₂ – Vi) = PΔV

dove: P è la pressione a cui avviene la reazione

ΔV è la variazione di volume associata alla reazione

Inoltre il sistema nel passare dallo stato iniziale (reagenti) allo stato finale (prodotti), subisce un aumento di volume corrispondente allo sviluppo di H2(_g) in quanto il volume dei componenti allo stato condensato non varia apprezzabilmente.

Quindi ai fini della valutazione del lavoro meccanico che un sistema in evoluzione può compiere, interessa la variazione di volume delle sostanze in fase gas.

Per i gas esiste una proporzionalità diretta tra volume e numero di moli per cui possiamo scrivere:

ΔVc∞ Δn

essendo ΔV il volume di idrogeno sviluppato

n il numero di moli di idrogeno sviluppato

Ammettendo che H_2(g) nelle condizioni di reazione si comporti idealmente, possiamo applicare l’equazione di stato dei gas perfetti, cioè:

PΔV= ΔnRT

ma, essendo PV = W, si ha: W= ΔnRT
Dalla stechiometria della reazione, risulta evidente che il numero di moli di H2(g) formatosi è pari a quello di moli di Zn reagite e queste si ottengono facilmente come segue:
massa di Zn reagita /PA_Zn= moli di Zn = moli di H2(g)

I dati numerici disponibili sono:
m= 10 g
PA = 65,37 g
R = 1,98 cal/(mol K)

T= 298,15K
Sostituendo si ha:
10 g x 1,98ca/mol K  x  298,15 K /  65,37 g / mol   =  = 90,31 cal
La variazione di energia è :
ΔΕ = Q-W = —5200 cal – (90,31 cal) = —5109,69 cal corrispondenti a – 21393,3 J.

 8-   30 g di n-ottano vapore vengono compressi alla temperatura di condensazione di 125,7 °C fino a formare n-ottano liquido.
Calcolare il volume iniziale e quello finale, il calore ceduto dall’ n-ottano vapore nel condensarsi, il lavoro compiuto sullo stesso e la variazione di energia interna associata a tale trasformazione sapendo che, la pressione di equilibrio è di 1 atm, il calore latente molare alla temperatura di condensazione è di 8110 cal/ mol e la densità del n-ottano liquido nelle medesime condizioni è di 0,680 g/cm3.

soluzione

La trasformazione considerata è la seguente:
n-ottano vapore —-> n-ottano liquido
Ammettendo un comportamento ideale dell’n-ottano vapore nelle condizioni considerate, possiamo calcolare il volume iniziale utilizzando l’equazione di stato dei gas perfetti, cioè:
PV= nRT     V=nRT/P

con n = m/PM
l’ottano di formula bruta C8H18 ha peso molare :

PM= 114,23   quindi n= 30 g / 114,23 g/mol = 26,26 x 10^-2 mol

sappiamo dai dati che :

P= 1 atm

T= 125,7 +273,15 = 398,85 K

R= 0,0821 litri atm /mol K    per cui il volume di n-ottano allo stato di vapore è:

V=nRT/P = 8,59 litri

il n-ottano alla fine si trova allo stato liquido per cui il volume finale si ottiene dalla densità, infatti

d=m/V  ed essendo d= 0,680 g/ ml si ha    V= 30 / 0,680 = 0,044 litri

La variazione di volume ΔV  è pertanto

ΔV= V _finale – V_iniziale = 0,044 – 8,59 = -8,55 litri 

ciò significa che il processo avviene con diminuzione di volume e si compie un lavoro paria a

L = PΔV in quanto la pressione rimane costante.

L= 1 x -8,55 = -8,55 litri atm pari a -862,55 J quindi 206,26 cal

Per calcolare il calore ceduto durante la trasformazione ricordiamo che

1 mole condensando cede 8110 cal ed essendo le moli 26,26 x 10 ^-2  si ha:

Q =  8110 x 26,26 x 10 ^-2  = 2129,69 cal

Poiché abbiamo calcolato sia Q che L allora possiamo calcolare ΔE

ΔΕ = Q – L  = -2129,69 – ( -206,26 ) =  -1923,43 cal

9- Consideriamo la combustione completa di 100 g di acido oleico (C18H3402) alla pressione di 1 atm e alla temperatura di 20 °C. Calcolare la variazione di energia interna associata alla trasformazione nonché il lavoro compiuto dal sistema sapendo che nella combustione completa di I mole di acido oleico si liberano 2657,4 kcal.

soluzione

La reazione di combustione totale dell’acido oleico è la seguente:
2C₁₈ H₃₄O₂(l) + 51 O2(g) —> 36CO2(g) + 34H2O(l)
Lo stato fisico dell’acido oleico alle condizioni di reazione è quello liquido e la stessa cosa può dirsi per l’acqua formatasi, mentre l’ossigeno e l’anidride carbonica si ritrovano allo stato gassoso.

Considerando del tutto trascurabile il volume delle sostanze liquide rispetto a quello delle sostanze gassose, la variazione di volume associata alla reazione di combustione sarà:
ΔV = Vfinale – Viniziale≅   V_CO2  – V_O2
Ma per i gas esiste una proporzionalità diretta tra volume e numero di moli, per cui possiamo scrivere: ΔV= Δn

ndo che i componenti gassosi presenti nel sistema di reazione si comportino idealmente, si può applicare l’equazione di stato dei gas perfetti, cioè:
PΔV= Δn RT
ove il primo membro altro non è che il lavoro associato alla trasformazione considerata. Per cui si ha:
W= Δn RT
A questo punto è necessario dedurre la variazione del numero di moli naturalmente riferita solo ai componenti gassosi che sono O2 e CO2.
Il numero delle moli di O2 reagite ed il numero di moli di CO2 formatesi, possono essere calcolati dalle moli di acido oleico che subiscono la combustione.
Le moli di acido oleico che reagiscono sono pari a quelle poste a reagire, in quanto la reazione è completa.
Il numero di moli di acido oleico è dato da:

n_acidol = massa _aciol / PM_acidol

n_acidol= 100/ 282,47 = 0,354 mol

n_O2 = 51 x 0,354 /2 = 6,372 mol

n_CO2 = 36 x 0,354 /2 = 6,372

la variazione del numero di moli è

Δn = (6,372 -9,027) = – 2,655 mol

Come si può osservare la variazione del numero di moli, relative ai componenti gassosi presenti nel sistema di reazione, è negativa e ciò è in accordo col fatto che la reazione decorre con diminuzione di volume

W=Δn RT
Δn = — 2,655 mol
T= (20 + 273,15)K = 293,15K
Sostituendo i dati numerici, si ottiene:
W = —2,655 mol x 1,98 cal/ mol K x 293,15K
che corrispondono a – 1541,06 cal.

La variazione di energia interna del sistema si può dedurre, tenendo presente che 1 mole di acido oleico per combustione, come risulta dalla reazione sopra riportata, libera 2657,4 kcal ed utilizzando l’espressione del primo principio della termodinamica. La quantità di calore sviluppato dalla combustione di 100 g di acido oleico, cioè 0,354 mal, è data da:
2657,4 kcal’ mol-1 0,354 mol = 940,72 kcal Essendo un calore ceduto dal sistema, si ha:

Q = — 940,72 kcal
La variazione di energia interna è quindi pari a:

ΔΕ= Q— W
cioè:
ΔΕ= 940,72 kcal – (— 1541,06 cal) —940,72 kcal + 1,54 kcal = — 939,l8 kcal

10-Si consideri la seguente reazione:

CaCO3 , -. CaO + CO2 (g)

Il calore richiesto per la decomposizione di 1 mole di carbonato di calcio alla pressione di 1 atm e alla temperatura di 800 °C è pari a 41,5 kcal.
Calcolare la variazione di energia interna del sistema nel caso in cui la quantità di carbonato posta a reagire è di 80 g ed ammettendo che la conversione ponderale della reazione di decomposizione è del 90%.

soluzione

La quantità di carbonato di calcio che si decompone è:
80g  al 90 % cioè  80 x 0,90 = 72g
Il numero di moli di carbonato di calcio che si decompone è perciò:
n _CaCO3 = 72/ 100,09 =71,94 x 10^-2
La quantità di calore richiesta per la decomposizione termica di 71,94 10^-2 mol di carbonato di calcio si ottiene come segue:
Q = 71,94 x 10^-2 mol 41,5 kcal /mol = 29,86 kcal
Il segno positivo è in accordo col fatto che per convenzione il calore che entra nel sistema è positivo.

Il lavoro meccanico associato a variazioni di volume, per la reazione di decomposizione, è dato da:
W= PΔV
La variazione di volume che subisce il sistema nel passare dai reagenti ai prodotti, considerando del tutto trascurabile il volume dei componenti allo stato solido rispetto a quello della anidride carbonica, è pari in pratica al volume occupato dall’anidride carbonica alla temperatura ed alla pressione a cui avviene la decomposizione. Perciò:

ΔV= V_CO2
Inoltre, ammettendo che nelle condizioni di reazione l’anidride carbonica si comporti idealmente, si può applicare l’equazione di stato dei gas perfetti, cioè:
PΔV=ΔnRT
Per quanto detto sopra, possiamo perciò scrivere: W= Δn RT
La variazione del numero di moli, naturalmente riferita solo ai componenti gassosi, coincide col numero di moli di anidride carbonica formatasi e può essere dedotta dalle moli di carbonato di calcio reagite effettivamente e tenendo presente la stechiometria della reazione. Quindi si ha:
n_CaCO3 = n_CO2 =Δn = 71,94 x 10^-2 mol
I dati di cui disponiamo sono

Δn = 71,94 10-2  mol
R = 8,31434  J /mol K
T= (800 + 273,15) K = 1073,15 K
Sostituendo, si ottiene:
W= 71,94 x 10^-2 x 8,31434 x  1073,15  = 6418,87 J

tenendo conto che 1 Jaule corrisponde a 4,187 cal 6418,87 J  corrispondono  a 1533 cal, cioè 1,53 kcal.
La variazione di energia interna è data da ΔΕ = Q – W     o ΔΕ = Q – L  ed essendo
Q = 29,86 kcal W= 1,53 kcal
Sostituendo si ottiene:
ΔΕ= 29,86— 1,53 = 28,33 kcal

11-   100 dm³ di una miscela idrocarburica gassosa, contenente metano (CH4) ed etano (C2H6), viene fatta reagire con ossigeno alla pressione costante di 1 atm. Il volume di CO2 sviluppato, misurato a 1 atm e 20 °C è pari 160 dm³.
Calcolare la composizione della miscela nonché la variazione di energia interna e il lavoro associato alla reazione, alla temperatura ed alla pressione sopra citate, ammet­tendo che la stessa sia completa e utilizzando la quantità teorica di ossigeno richiesto.

soluzione

Il calore di combustione di ciascuno dei componenti la miscela idrocarburica alle condizioni di temperatura e pressione indicate è:
ΔΗ_{c etano}= – 372,820 kcal/mol
ΔΗc _metano = – 212,798 kcal /mol
La combustione della miscela idrocarburica può essere rappresentata dalle seguenti reazioni:
CH4 + 2O2(g)          –>  CO2(g) + 2H2O(l)
2C2H6(g)+7O2(g)  –> 4 CO2(g) + 6 H2O(l)

Data la proporzionalità tra volume e numero di moli, per i gas, possiamo dire che  1 dm³ di metano reagisce con 2 dm³ di O2 per dare 1 dm³ di CO2, mentre la combustione completa di 2 dm³ di etano richiede 7 dm³ di O2 e dà origine a 4 dm³ di CO. Naturalmente in entrambe le reazioni si forma H2O che a 20 °C e 1 atm si trova allo stato liquido ed occupa un volume del tutto trascurabile rispetto a quello dei componenti gassosi.
Indicando con x e y rispettivamente i decimetri cubi di metano e di etano presenti nella miscela idrocarburica iniziale e tenendo conto della stechiometria delle reazioni sopra citate, possiamo scrivere;
volume della miscela iniziale = x + y

volume di CO2 = x + 2y
Sostituendo i dati numerici, si ha;
100  = x+ y                x=40 dm³
160  =x+2y                y=60 dm³

Perciò la miscela idrocarburica messa a reagire ha la seguente composizione percentuale in volume;
40% di metano e 60% di etano.
La variazione di volume che subisce il sistema reagente è data da: V= V_fin — Vi_niz
dove:
Vf = volume della miscela alla fine della reazione ad 1 atm e a 20 °C
Vi = volume della miscela di reazione all’inizio della reazione ad 1 atm e a 20 °C
ma
Vf = V_miscela + V_O2

Vi= V_CO2 + V_H2O 
VmisceIa = volume della miscela idrocarburica messa a reagire
V_O2 = volume di ossigeno teoricamente richiesto
VH2O = volume di H2O liquida formatasi dalla reazione di combustione.
Il volume di ossigeno richiesto dalla reazione si deduce facilmente tenendo presente quanto detto sopra a proposito dei rapporti di combinazione, cioè possiamo scrivere:
V_O2= 2x 40 dm³ + 3,5 x  60 dm³= 290 dm³
Il volume della miscela all’inizio della reazione e quello alla fine sono, rispettivamente:
Viniz= 100 dm³ +290 dm³  = 390 dm3
Vfin = 160 dm³ + V_H2O
ed essendo  V_H2O  < < 160 dm³ risulta:
ΔV= 160 dm³ —(390  dm³) = —230 dm³
Il lavoro associato alla trasformazione considerata, tenendo presente che decorre a pressione costante è dato dalla relazione:
W= PΔV

Sostituendo i dati numerici disponibili, si ottiene: W = 1atm'(-230 dm³) = —230 dm³ atm
che corrispondono a — 23303 J
La variazione di energia interna, può essere dedotta solo dopo aver calcolato il calore liberato dalla combustione della miscela. Ammettendo che il calore di combustione Q di una miscela gassosa sia una proprietà additiva, si può scrivere;
Q_comb = n_metano  x  ΔΗc _metano  + n_etano x ΔΗ_{c etano} 

 n_metano e n_etano  si possono ottenere applicando l’equazione di stato dei gas perfetti, naturalmente ammettendo che sia i singoli componenti che la miscela idrocarburica si comportino idealmente. Cioè;
PV = nRT  da cui sostituendo i valori numerici si ottiene

n_etano  = 2,496mol
n_metano = 1,664 mol

Il calore sviluppato dalla combustione completa di 100dm³ di miscela idrocarburica è perciò:

Q_comb = n_metano  x  ΔΗc _metano  + n_etano x ΔΗ_{c etano} 

 cioè:
Q_comb  = 2,496 mol x (— 372,820 kcal/mol) + 1,664 mol x (— 212,798 kcal/mol) =  – 1284,6 kcal
La variazione di energia interna associata alla trasformazione è

ΔΕ = Q – W 0        ΔΕ= Q -L
I dati numerici sono: Q = – 1284,6 kcal
W=-23303 J pari a -5,6kcal
Sostituendo, si ottiene:
ΔΕ = —1284,6 kcal – (-5,6 kcal  ) = —1279 kcal

12-   I ΔΗ di formazione per CO2 (g), H2O(g) e C2H6(g) sono rispettivamente -393,5  kJ, .285,8 kJ e -84,5 kJ. Calcolare il calore prodotto nella combustione di 1 kg di etano.

soluzione

la reazione di combustione è :

C2H6(g) +7/2 O2(g) → 2CO2(g) + 3H2O(aq)

essendo ΔΗ° di reaz. = ∑ΔΗ°_prodotti -∑ΔΗ°_reagenti

ΔΗ° di reaz. = 3 x (-285,8) + 2 x (- 393,5) – (-84,5) = -1560 kJ

questo risultato è realtivo ad 1 mole di C2H6 e per conoscere quanto calore si ottiene da 1 Kg calcoliamo le moli corrispondenti che sono : moli etano= 1000g / 30= 33,3 moli 

si deduce che se 1 mole produce -1560 kJ 33,3 moli ne produrranno X   da cui X= 33,3 x -1560 kJ = – 52000 kJ = -5,2 x 10⁴  KJ

13-Si ottiene piu’ calore dalla combustione di 1 L di ottano (C8H18, d = 0.703 g/mL) o di 1 m³
di metano (misurato a 20°C e 1,1 atm)? ∆H°form CO2 (g) = -394 kJ/mol, ∆H°form H2O(l) = – 286 kJ/mol; ∆H°form ottano(l) = – 189 kJ/mol; ∆H°form CH4 (g) = – 74,9 kJ/mo

soluzione

le reazioni di combustione sono:
C8H18 + 25/2 O2 = 8 CO2 + 9 H2O

CH4 + 2 O2 = CO2 + 2 H2O

∆H°comb C8H18= [9 x (- 286) + 8 x (-394) – (-189)] kJ/mol = – 5537 kJ/mol, calore ottenuto da 1 mol di
ottano
∆H°comb CH4= [2 x (- 286) + (-394) – (-74,9)] kJ/mol = – 891,1 kJ/mol, calore ottenuto da 1 mol di
metano
Ora occorre verificare a quante moli corrispondono le quantità indicate dei due combustibili.
Ottano: (1000 mL x 0.703 g/mL) : 114,2 g/mol = 6,16 mol; 6,16 mol x (- 5537 kJ/mol) = 3,41 x 10⁴ kJ
Metano: (1000 L x 1,1 atm) : (0,082 atm L ^-1 mol^-1x 293 K) = 45,8 mol;
45,8 mol x (- 891,1 kJ/mol) = 4,08 x 10⁴ kJ
Quindi si ottiene leggermente più calore da 1 m³ di metano che da 1 L di ottano.

14- Un corpo di ferro di massa 110 g, inizialmente a 95°C, viene immerso in 0,400 kg di acqua a 22,0°C. Quale temperatura viene raggiunta all’equilibrio?

La capacità termica del ferro è 0,450 J K^-1 g^-1 e quella dell’acqua è 4,184J K^-1 g^-1.

A) 34°C

B) 24°C

C) 44°C

D) 54°C

soluzione

Quando un corpo di massa m₁, alla temperatura T₁, viene messo in contatto termico con un altro corpo di massa m₂, alla temperatura T₂ diversa da T₁, ha luogo un passaggio di calore dal corpo a temperatura più alta a quello a temperatura più bassa. Il flusso di calore termina non appena i due corpi hanno la stessa temperatura T₀, cioè hanno raggiunto l’equilibrio termico. Se non vi sono perdite di calore nell’ ambiente esterno,(sistema adiabatico) tutto il calore ceduto dal corpo più caldo viene assorbito da quello più freddo. In questo caso la temperatura T₀ di equilibrio risulta

dove c₁ e c₂ sono i calori specifici dei due corpi.

110 x 0,450 x 95 + 400 x 4,184 x 22 / 110 x 0,450 + 400 x 4,184 = Teq

4702.5 + 36819/1722,5  =24,1°C

risposta corretta B

15- L’equilibrio di formazione dell’acqua

2 H2(g) + 02(g)  ⇄ 2 H20(g)

si sposta a destra se la temperatura diminuisce. Si può quindi concludere che: 

A) la reazione ha un ΔH maggiore di zero

B) la reazione è endotermica

C) la reazione è esotermica

D) non si può trarre alcuna conclusione in assenza di dati aggiuntivi

soluzione

in una qualunque reazione come ad es A+B ⇄ C+D.

∑ΔH_prodotti – ∑ΔH_regenti =ΔH_reazione

se pertanto ∑ΔH_prodotti > ∑ΔH_regenti  allora  il  ΔH_reazione è positivo

se invece      ∑ΔH_prodotti < ∑ΔH_regenti  allora  il  ΔH_reazione è negativo

poiché se ΔH_reazione = -Q  (dove Q= quantità di calore)

se ΔH_reazione è negativo la reazione è esotermica cioè viene prodotto calore

se ΔH_reazione è positivo la reazione è endotermica e perchè avvenga deve assorbire calore

quindi  se A+B→ C     +Q  (ΔHnegativo )   reazione esotermica

              se A+B  → C     -Q  (ΔHpositivo )   reazione endotermica

allora nel caso della formazione dell’acqua 

2 H2(g) + 02(g)  ⇄ 2 H20(g)

L’entalpia di formazione è la variazione di entalpia che accompagna la formazione di una quantità di sostanza a partire dai suoi elementi.

La variazione di entalpia ΔH  dipende da  Temperatura,Pressione stato fisico dei reagenti e dei prodotti ( solido, liquido, gassoso, acquoso).

Naturalmente se la reazione avviene con produzione di calore (esotermica)

A+B→C  +Q

un aumento di calore Q sposta l’equilibrio verso sinistra mentre una sottrazione di calore (temperatura più bassa) sposta l’equilibrio verso destra.

ovviamente se la reazione avviene con assorbimento di calore (endotermica)

A+B  →C  -Q

è evidente che l’aumento di calore Q sposta l’equilibrio verso destra

Pertanto se la temperatura diminuisce la reazione e l’equilibrio si spostano a sinistra

da quanto detto, per la reazione del quesito, e poichè la diminuzione di temperatura provoca uno spostamento verso destra della reazione, allora la reazione è Esotermica.

Risposta corretta C

18-Un sistema adiabatico si espande da 1,0 m3 a 1,3 m3 contro una pressione esterna costante pari a 1,00 x 104. Pa. Qual è la variazione di energia interna?

A) ΔE = -3,0 kJ

B)ΔE = -30 kJ

C) ΔE =  30kj

D) ΔE = -40 kJ

soluzione

il primo principio della termodinamica è ΔE = Q + Lavoro

Al lavoro compiuto dal sistema per convenzione si attribuisce un valore negativo e si misura in Jaules

Nelle trasformazioni adiabatiche non c’è scambio di calore con l’esterno per cui Q=0

ΔE=L=- P(V2-V1) pertanto

L =- Pesterna (V2-V1)= – 1,00 x 104 x (1,3 -1) = -1,00 x 10⁴ x 0,3

ΔE = -1,00 x 10⁴ x 0,3 =3000 J  =  – 3,0 KJ

risposta corretta A

19-Operando in fase gassosa e in opportune condizioni, si verifica l’equilibrio cicloesano/metilciclopentano con la seguente dipendenza della Keq dalla temperatura:

ln Keq = -(2059 / T) + 4,814

Individuare le variazioni di entalpia, entropia ed energia libera di reazione in condizioni standard a 298,0 K (ΔH°, ΔS° e ΔG°).

A) ΔH°= 110,9 kJ; ΔS°= 34,06 J K-1 ; ΔG°= 22,33 kJ

B) ΔH°= 241,2 kJ; ΔS°= 49,03 J K-1 ; ΔG°= 146,3 kJ

C) ΔH°= 71,19 kJ; ΔS°= 20,02 J K-1 ; ΔG°= 166,3 kJ

D) ΔH°= 17,12 kJ; ΔS°= 40,03 J K-1 ; ΔG°= 5,202 kJ

soluzione

considerato che la relazione che lega lnK alla temperatura non è altro che l’ equazione di Van’t Hoff,

lnk =-ΔH/RT + ΔS/R  

 ΔS= 4,814 x 8,314 = 40,03 J K^-1

ΔH/R = -2059   ΔH=2059 x 8,314 =17,12 KJ 

ΔG= ΔH -T ΔS  

17120 – 298 x 40=5,2 KJ

risposta corretta D

20- Una mole di ammoniaca gassosa (peso molecolare M = 17 g/mol) passa dallo stato 1 (p1 = 4,0 atm, V1 = 10 litri allo stato 2 (p2 = 2,0 atm, V2 = 20 litri).
Calcolare: a) la variazione di energia interna, b) la variazione di densità, c) lavariazione di entropia.

soluzione

L’ammoniaca è tetraatomica, quindi cV = 3 R, pertanto:

$∆E= n Cv ∆T = 3n R \left(\right( p2V2 – p1V1) / n R =3( p2V2 – p1V1) = 0.$

La densità di un gas perfetto è data da
ρ =pM/ RT

$$\begin{gathered} ∆\rho =\rho 2 – \rho 1= M/R (P2/T2 –P1/T1)= M/R(P2–P1/T) \\ ∆\rho = M/R(P2–P1)/P1V1/nR \\ \mathbf{∆}\mathit{\rho }\mathbf{ }\mathbf{=}\mathit{M}\mathbf{(}\mathit{P}\mathbf{2}\mathbf{–}\mathit{P}\mathbf{1}\mathbf{)}\mathbf{/}\mathit{P}\mathbf{1}\mathit{V}\mathbf{1} \end{gathered}$$

Δρ = – (17 x 10^-3 x  2 x 1,01 x 10⁵) /(4 x 1,01 x 10⁵ x 10^-2) = -0,85 Kg/m³

la variazione di entropia come
ΔS = n R lnV2 /V1 = R ln2 = 5,76 J/K

21-  Per un solido di massa m risulta, in un dato processo, ΔS = k ΔT, con k costante.

a) Ricavare la dipendenza del calore specifico c dalla temperatura;

b) utilizzando tale relazione, calcolare k e la quantità di calore necessaria per riscaldare un solido di massa m = 300 g da t1 = 27 °C a t2 = 77 °C, sapendo che C (27 °C) = 0,3 cal /g °C.
soluzione

Per ricavare k, ricordiamo che

dS = k dT = dQ/T =m C dT /T

 C =k T/ m

quindi possiamo scrivere

$$\begin{gathered} \mathit{Q}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}\mathbf{ }}\mathit{m}\mathbf{ }\mathit{C}\mathbf{ }\mathit{d}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}\mathbf{ }}\mathbf{ }\mathit{k}\mathit{T}\mathbf{ }\mathit{d}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{K}\mathbf{/}\mathbf{2}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{ }{\mathit{T}}^{\mathbf{2}}\mathbf{2}\mathbf{ }\mathbf{–}\mathbf{ }{\mathit{T}}^{\mathbf{2}\mathbf{ }}\mathbf{1}\mathbf{ }\mathbf{)}\mathbf{.} \\ \mathit{k}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{m}\mathit{C}\mathbf{/}\mathit{T}\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{,}\mathbf{3}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{0}\mathbf{,}\mathbf{3}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{4186}\mathbf{/}\mathbf{ }\mathbf{300}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{1}\mathbf{,}\mathbf{26}\mathbf{ }\mathit{J}\mathbf{/}\mathit{K} \end{gathered}$$

$Q= 1,126/2 ({350}^2 – {300}^2 ) = 20,5 KJ$

22- . Un blocco di ferro (cFe= 0,11 cal/(g °C) di massa m1 = 100 g viene immerso in una massa d’acqua m2 = 200 g contenuta in un recipiente di vetro[(cv = 0,12 cal/(g °C)] di massa m3 = 300 g. Trascurando ogni dispersione di calore, se la temperatura dell’acqua e del recipiente di vetro sale da t1 = 15°C a t2 = 24 °C, a) qual era la temperatura iniziale del blocco di ferro? b) qual è statala variazione di entropia dell’acqua?

soluzione
Il blocco di ferro cede calore all’acqua e al vetro, e la temperatura di equilibrio è:

$$\begin{gathered} {\mathit{T}}_{\mathbf{e}\mathbf{q}\mathbf{u}}\mathbf{=}\mathbf{(}\mathbf{ }\mathit{m}\mathbf{1}{\mathit{C}}_{\mathbf{f}\mathbf{e}\mathbf{ }}\mathit{X}\mathbf{+}\mathit{m}\mathbf{2}\mathbf{ }{\mathit{C}}_{\mathbf{H}\mathbf{2}\mathbf{O}}\mathbf{ }\mathit{T}\mathbf{1}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{m}\mathbf{3}\mathbf{ }{\mathit{C}}_{\mathbf{v}\mathbf{e}\mathbf{t}\mathbf{r}\mathbf{o}}\mathbf{ }\mathbf{)}\mathit{T}\mathbf{1}\mathbf{/}\mathbf{ }\mathbf{ }\mathit{m}\mathbf{1}{\mathit{C}}_{\mathbf{f}\mathbf{e}}\mathbf{ }\mathbf{+}\mathit{m}{\mathbf{2}}_{\mathbf{ }\mathbf{C}\mathbf{H}\mathbf{2}\mathbf{O}}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{m}\mathbf{3}\mathbf{ }{\mathit{C}}_{\mathit{v}etro } \\ \mathit{X}\mathbf{=}\mathbf{(}\mathbf{ }\mathit{m}\mathbf{1}{\mathit{C}}_{\mathbf{fe}\mathbf{ }}\mathbf{+}\mathit{m}\mathbf{2}\mathbf{ }{\mathit{C}}_{\mathbf{H}\mathbf{2}\mathbf{O}}\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }\mathit{m}\mathbf{3}\mathbf{ }{\mathit{C}}_{\mathbf{vetro}}\mathbf{ }\mathbf{)}{\mathit{T}}_{\mathbf{e}\mathbf{q}\mathbf{u}}\mathbf{ }\mathbf{–}\mathbf{ }\mathbf{(}\mathit{m}{\mathbf{2}}_{\mathbf{ }\mathbf{CH}\mathbf{2}\mathbf{O}}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{m}\mathbf{3}\mathbf{ }{\mathit{C}}_{\mathbf{v}\mathbf{e}\mathbf{t}\mathbf{r}\mathbf{o}\mathbf{ }}\mathbf{)}\mathbf{/}\mathbf{ }\mathit{m}{\mathit{C}}_{\mathbf{f}\mathbf{e}} \\ \mathit{X}\mathbf{=}\mathbf{ }\mathbf{217}\mathbf{,}\mathbf{1}\mathbf{ }\mathbf{°}\mathit{C} \\ \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{m}\mathbf{2}\mathit{C}\mathbf{ }\mathbf{ln}\mathbf{ }\mathit{T}\mathbf{2}\mathbf{/}\mathit{T}\mathbf{1}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{,}\mathbf{2}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{4186}\mathbf{ }\mathbf{ln}\mathbf{ }\mathbf{297}\mathbf{,}\mathbf{15}\mathbf{/}\mathbf{288}\mathbf{,}\mathbf{15}\mathbf{=}\mathbf{25}\mathbf{,}\mathbf{75}\mathbf{ }\mathit{J}\mathbf{/}\mathit{K} \end{gathered}$$

22- . 1 mol di gas perfetto monoatomico passa reversibilmente dallo stato A (1atm,1 l) allo stato B (3 atm,3 l) lungo una trasformazione rettilinea AB. Calcolare:

a) il lavoro compiuto sul gas,

b) la quantità di calore scambiata,

c) la variazione di entropia. 

soluzione

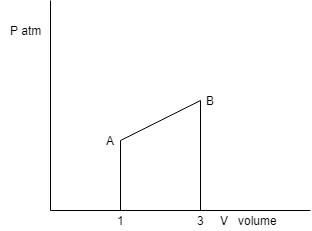Il lavoro nel piano (p,V) è dato dall’area sottesa dal profilo della trasformazione, ovvero dall’area del trapezio AB31:

L = 0,5 . 4 . 2 = 4 l atm = 404 J.

Q = L + ΔΕ = L + n C_V (TB – TA ) = L + n Cv (P_BV_B – P_AV_A) / nR =L +3/2 ( P_BV_B – P_AV_A ) = 404 + 1,5 x 8 x 101 = 1, 62 kJ

ΔS = n R lnV_B/V_A + nCv ln T_B / T_{A =n R ln 3 + 3/2  nR lnPBVB/ PAVA} = 4n R ln 3 = 36,5 J/K

23- 13.46. Un boiler elettrico di potenza W = 2 kW riscalda una massa d’acqua m = 80 kg da t1 = 12 °C a t2 = 60 °C. Supponendo nulla ogni dispersione, calcolare:
a) il tempo impiegato,

b) la variazione di entropia dell’acqua,

c) la variazione di entropia della sorgente (la resistenza elettrica), sapendo che essa, durante il riscaldamento, si mantiene costantemente alla temperatura t3 = 70 °C,

d) la variazione di entropia dell’universo.

soluzione

sapendo che

Q = m c (t2 – t1) = W t1                  t =m c( t2- t1)  /W  = 80 x 4180  x 48  / 2000   =  8025, 6 s = 2 h14 min.         

$$\begin{gathered} \mathbf{∆}\mathit{S}\mathbf{=}\mathbf{\int }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}}\mathit{m}\mathbf{ }\mathit{c}\mathbf{ }\mathit{d}\mathit{T}\mathbf{/}\mathit{T}\mathbf{=}\mathbf{ }\mathit{m}\mathbf{ }\mathit{c}\mathbf{ }\mathit{l}\mathit{n}\mathbf{ }\mathit{T}\mathbf{2}\mathbf{/}\mathbf{(}\mathit{T}\mathbf{1} \\ \mathbf{∆}\mathit{S}\mathbf{=}\mathbf{80}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{41280}\mathbf{ }\mathit{l}\mathit{n}\mathbf{333}\mathbf{,}\mathbf{15}\mathbf{ }\mathbf{/}\mathbf{ }\mathbf{285}\mathbf{,}\mathbf{15} \\ \mathbf{∆}\mathit{S}\mathbf{=}\mathbf{ }\mathbf{5}\mathbf{,}\mathbf{2}\mathbf{ }\mathit{x}\mathbf{ }{\mathbf{10}}^{\mathbf{4}}\mathbf{ }\mathit{J}\mathbf{/}\mathbf{ }\mathit{K} . \end{gathered}$$

questo risultato è il ΔS del sistema acqua

La sorgente si mantiene a temperatura costante T3 = 343,15 K mentre cede all’acqua la quantità di calore Q, pertanto

$$\begin{gathered} \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{Q}\mathbf{ }\mathbf{/}{\mathit{T}}_{\mathbf{3}\mathbf{ }}\mathbf{=}\mathit{m}\mathbf{ }\mathit{c}\mathbf{(}\mathbf{ }{\mathit{t}}_{\mathbf{2}\mathbf{ }}\mathbf{–}\mathbf{ }{\mathit{t}}_{\mathbf{1}}\mathbf{)}\mathbf{ }\mathbf{/}\mathbf{ }{\mathit{T}}_{\mathbf{3}\mathbf{ }}\mathbf{ }\mathbf{=}\mathbf{80}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{4180}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{48}\mathbf{ }\mathbf{/}\mathbf{ }\mathbf{343}\mathbf{,}\mathbf{15} \\ \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{–}\mathbf{ }\mathbf{4}\mathbf{,}\mathbf{7}\mathbf{ }\mathit{x}{\mathbf{10}}^{\mathbf{4}}\mathbf{ }\mathit{J}\mathbf{/}\mathbf{ }\mathit{K}\mathbf{ }\mathbf{.} \end{gathered}$$

questo risultato è il ΔS dell’ambiente

L’universo termodinamico è costituito dalla sorgente e dal sistema (acqua), perciò
ΔS_universo = ΔS_amb + ΔS_sist = 5  kJ/K.

   Send article as PDF