La teoria del legame di valenza VB e la teoria VSEPR (valence shell electron pair repulsion) sono sufficienti per spiegare  la geometria delle molecole e la natura dei legami. Tuttavia per spiegare alcune proprietà quali ad esempio le lunghezze di legame uguali come in SO4^-2 si ricorre alla risonanza ma per spiegare il paramagnetismo dell’ossigeno nessuna delle suddette teorie risulta adeguata. Per dare una spiegazione a questo fenomeno e per comprendere meglio altre proprietà quali la natura degli spettri UV ed altre proprietà molecolari ricorriamo alla teoria degli orbitali molecolari. 
Il concetto di ORBITALE MOLECOLARE è una naturale estensione del trattamento degli orbitali atomici. Infatti, si assume che due orbitali sovrapponendosi formino una nuvola elettronica che si estende  tra i due atomi e quindi gli elettroni appartengono ad ambedue gli atomi e sono soggetti al potenziale di tutti i nuclei ed  alla distribuzione della carica degli altri elettroni. Per gli orbitali molecolari (OM) valgono le stesse restrizioni imposte agli orbitali atomici (AO) per esempio un OM può avere al massimo due elettroni e devono avere spin diversi. Anche gli OM devono essere normalizzati perchè la probabilità di trovare l’elettrone nell’OM è il 100 % e ricordando che Ψ² rappresenta la probabilità si deve avere  anche per l’OM che chiamiamo sempre Ψ

∫Ψ² dτ =1

e vale anche la condizione di ortogonalità :

∫Ψ_aΨ_b dτ = 0

Ciò permette di disegnare fisicamente i contorni delle costanti di probabilità intorno alla molecola e visualizzare le regioni in cui si ha la maggior o minore probabilità di trovare gli elettroni. Possiamo inoltre pensare che ogni OM Ψ sia soluzione dell’equazione di HARTREE- FOCK  :

FΨ = ε Ψ

F rappresenta l’amiltoniano di Hartree-Fock

che è simile all’equazione di Schrodinger per un solo elettrone ma che in questo caso tiene conto delle interazioni dei vari elettroni con i diversi nuclei e tra gli stessi elettroni.

Prima di procedere dobbiamo fare alcune considerazioni sugli

ATOMI CON PIU’ ELETTRONI

Hartree  ha pensato di approssimare “nel modo migliore possibile” la funzione d’onda che è soluzione dell’equazione di Schrödinger a N elettroni (problema la cui soluzione esatta è in pratica impossibile da ottenere se non con potentissimi computers) con un prodotto di funzioni d’onda a un elettrone che sono gli orbitali atomici. L’esempio più semplice è rappresentato dall’ atomo di elio che ha due elettroni.Infatti l’energia cinetica totale è

T = T1 +T2 =P²_x1 +P²_y1 +P²_z1  + P²_x2+P²_y2 +P²_z2 /  2m     (perchè consideriamo il sistema a 3 dimensioni)

e l’energia potenziale è     V = – 2e²/r₁ -2e²/r₂ + e²/r₁₂

pertanto sapendo che l’equazione d’onda tridimensionale è:

d²Ψ/dx² + d²Ψ/dy² + d²Ψ/dz²  +8π²m/ h² ( E-V) Ψ = 0

ed essendo che d²/dx² + d²/dy² + d²/dz²   si chiama operatore  Laplaciano che si indica con  ∇ ² avremo

∇ ² Ψ  + ( 8π²m/ h²) ( E-V) Ψ = 0  l’

Ricordiamoci che Ψ non ha significato fisico e che solo il prodotto tra Ψ e il suo complesso coniugato Ψ* (che non è altro che -iΨ )  cioè  ΨΨ* che indicheremo sempre con |Ψ²|.

(Il prodotto ΨΨ* è necessario per rendere reale il numero che ne risulta in quanto Ψ potrebbe assumere qualsiasi valore, anche immaginario).

Per il sistema a due elettroni visto sopra, l’equazione di Hartree-Fock è quindi:

(∇ ² + ∇ ² ) Ψ + ( 8π²m/ h²) ( E + 2e²/r₁ +2e²/r₂ + 2e²/r₁₂ )Ψ

l’ultimo termine V=e²/r₁₂  non è altro che il potenziale di repulsione tra i due elettroni.

Riassumendo diciamo che Hartree-Fock hanno proposto quindi un metodo per ridurre l’equazione di N elettroni ad una somma di equazioni monoelettroniche in grado di trovare una soluzione almeno approssimata all’equazione ad N elettroni.

Essi hanno adoperato un metodo detto SELF CONSISTEND FIELD (SCF) che consisteva nel prendere in considerazione una funzione Ψ  che tenesse conto delle interazioni tra elettroni e campo potenziale del nucleo ed il potenziale medio di tutti gli altri elettroni dell’atomo: questo portava ad un’equazione che poteva essere risolta numericamente da cui si poteva ottenere utilizzando un nuovo potenziale un  nuovo orbitale Ψ  che veniva sostituito nell’equazione per ottenere un altro dato numerico che serviva poi per ottenere una nuovaΨ e si ripeteva  il calcolo sino a che non si ottenevano almeno per due volte la stessaΨ.

Le   Ψ risultanti da questo calcolo possono essere utilizzate con delle approssimazioni dovute a Slater che ha quindi ottenuto delle Ψ che sono in buon accordo con quelle ottenute con il metodo SCF. Gli orbitali atomici dovuti a Slater ed utilizzati sono:

1s     Ne^-cr

2s     Nr e^-cr/2

2px   Nx^e-cr/2

3s      Nr² e^-cr/3

3Px    Nxre^-cr/3

N è il fattore di normalizzazione ( affinchè ∫ΨΨdτ =1 )

c è la carica nucleare effettiva c=Z -S      dove Z= numero atomico ed S= costante di schermo degli altri elettroni )

S=0 per tutti gli elettroni esterni al numero quantico principale considerato

S= 0,35  per ogni elettrone dello stesso numero quantico

S=0,30 è usato per l’elettrone 1s

se l’orbitale considerato è un orbitale s o p allora S=0,85 per ogni elettrone  che si trova nello strato vicino mentre S=1,00 per ogni elettrone ulteriore nello stesso strato.

In definitiva si può calcolare facilmente che la carica nucleare effettiva Z

per il carbonio è

C1s =5,70    C2p= 3,25

per l’azoto N è

N2p = 3,90

per l’ossigeno O è

O2p= 4,55

Adesso sappiamo quali siano le espressioni matematiche di Ψ1s Ψ2s ecc. quindi vediamo come  esse vengono utilizzate nel calcolo degli orbitali molecolari.

Prendiamo come esempio la molecola di idrogeno H2 : essa contiene 2 elettroni ognuno proveniente da un atomo H  e che contribuiscono a formare la molecola . Poichè non possiamo distinguere a quali atomi gli elettroni appartengano nella molecola, facciamo una semplificazione razionale: supponiamo che quando un elettrone si trova vicino all’atomo A la funzione d’onda sia Ψa  cioè la funzione d’onda che descrive l’elettrone sull’atomo A e che quando un elettrone si trova vicino all’atomo B la funzione d’onda sia Ψb.

Possiamo quindi ragionevolmente pensare che la combinazione lineare degli orbitali  Ψa e Ψb possano rappresentare l’orbitale molecolare  Ψm o meglio semplicemente Ψ. Pertanto :

 Ψ = Ca Ψa + Cb Ψb

  Ψ = Ca Ψa – Cb Ψb

in cui Ca e Cb rappresentano l’entità del contributo dei due orbitali atomici nella formazione della molecola. Ovviamente se vi sono più atomi allora l’OM sarà:

 Ψ = Ca Ψa + Cb Ψb + Cc Ψc + ….CnΨn

o meglio

dove con   χ_i  indichiamo gli orbitali atomici al posto di Ψ.

Il metodo descritto sopra è la cosiddetta approssimazione LCAO  (linear combination of atomic orbitals).

Le funzioni d’onda, utilizzabili con questo metodo, devono avere più o meno la stessa grandezza di energia.

Per calcolare l’energia dell’OM dato sopra occorre sostituire la funzione Ψ molecolare nell’equazione d’onda

H Ψ = EΨ   

moltiplichiamo ambedue i termini per  Ψ* ed integriamo. Avremo:

$\int \psi H\psi *\delta \tau = \int E \psi \psi *\delta \tau = E\int \psi \psi *\delta \tau$

da cui

$E= \int \psi H\psi *\delta \tau /\int \psi \psi *\delta \tau$

e sostituendo a Ψ la funzione OM che riscriviamo per comodità sostituendo a a Ca e b a Cb

Ψ = a Ψa + b Ψb

si ha

E= ∫ a Ψa + b Ψb H a Ψa + b Ψb dt / ∫ (a Ψa + b Ψb ) (a Ψa + b Ψb) dt

e sviluppando si ha 

$\int a\psi *aHa\psi a dt + \int a\psi *aHb\psi b dt + \int b\psi *bHa\psi a dt +\int b\psi *bHb\psi b dt /\int a\psi *a a\psi a dt +\int a\psi *a b\psi b dt +\int b\psi *b a\psi a dt +\int b\psi *b b\psi b dt$ ${a}^2\int \psi {*}_{a}H {\psi }_a dt + ab\int \psi {*}_{a}H {\psi }_b dt + ba\int \psi {*}_b H {\psi }_a dt + b^2\int \psi {*}_{b }H {\psi }_{b }dt / a^2\int \psi {*}_a{\psi }_a dt + ab \int \psi {*}_a {\psi }_b dt + ba\int \psi {*}_b{\psi }_a dt + b^{2 }\int \psi {*}_b{\psi }_b dt$

ponendo

Haa  = ∫  ΨaHΨadt              Hab= ∫ ΨaHΨbdt       

Hba =  ∫  ΨbHΨadt              Hbb = ∫ ΨbHΨbdt 

Saa    =∫  ΨaΨadt                   Sab = ∫ ΨaΨbdt       

Sba   = ∫  ΨbΨadt                  Sbb =∫ ΨaHΨadt

possiamo scrivere

 E = a² Haa + ab Hab  + ba Hba +b² Hbb  / a² Saa  + ab Sab + ba Sba + b² Sbb

I valori di a e b che rendono minima l’energia (più bassa è l’energia del legame più stabile è la molecola) si ottengono derivando l’equazione scritta sopra prima rispetto ad a poi rispetto a b ed eguagliando a zero

δE/δa =0

δE/δb =0

ricordando che la derivata di una frazione è data da

d/da =  [(derivata del numeratore rispetto ad a) x  (il denominatore non derivato)   –  (il numeratore non derivato)  x (la derivata del denominatore)] / (denominatore )²

a (H_aa-S_aaE) + b (H_ab -S_abE) =0

a(H_ba-S_baE) + b(H_bb– S_bbE) =0

Possiamo riscrivere  più semplicemente le equazioni  nel seguente modo:

a∫Ψa (H-E)Ψa dt +b ∫Ψa (H-E)Ψb dt =0

a∫Ψb (H-E)Ψa dt + b ∫Ψb (H-E)Ψb dt =0

questo risulta in due equazioni:

a (H_aa-E) + b (H_ab -E S_ab) =0

a(H_ba – E S_ba) + b( H_bb – E ) =0

noi siamo interessati a soluzioni in cui a e b devono essere diversi da zero,  quindi  è necessario che il determinante

      |    Haa -E           Hab -ESab |

      |  Hba-ESba       Hbb – E       |          =0

 (sia uguale a zero).

questo determinante viene chiamato DETERMINANTE SECOLARE  e una volta risolto

(H_aa-E ) (H_bb-E) – (H_ab-ES_ab)(H_ba-ES_ba) =0  

se poniamo adesso

Haa= Hbb= α

Hab=Hba = β è chiamato integrale di scambio e rappresenta la parte di energia dovuta ad entrambi i nuclei sugli elettroni

Saa =Sbb = 1

Sab= Sba=0  è chiamato integrale di sovrapposizione  

la figura mostra la sovrapposizione quando S=0 quando S <<1    e quando S di poco<1

il determinante scritto sopra diviene :

e dividendo tutto per  β

|α-E/β        1 | 

|  1       α-E/β |     =0        e  ponendo  α-E/β  = X 

risolvendo il determinante  si ha

X² -1 =0  cioè   X=1     X=-1 pertanto   α – E1/β = -1  da cui E1 = α + β

Pertanto l’energia associata a Ψ1    è  E =   α + β in questo caso l’orbitale è chiamato “bonding“

l’energia associata  a Ψ2 è  E=  α – β in questo caso l’orbitale è detto “antibonding”

possiamo adesso indicare in un diagramma le energie degli orbitali al variare della distanza nucleare

quì di seguito possiamo vedere l’andamento della funzione d’onda di legame in un piano ideale che passa per l’asse di legame (che unisce i due nuclei) e la funzione di antilegame :

le superfici di contorno per l’orbitale di legame e quello di antilegame sono indicate nelle figure sopra.

Nel caso dell’idrogeno si ha il seguente diagramma di energia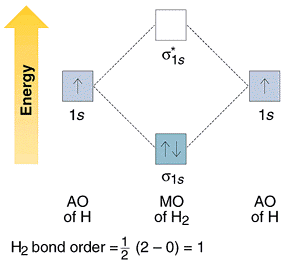

come si vede, gli elettroni provenienti dai due atomi di idrogeno adesso occupano l’orbitale a più bassa energia (orbitale σ ) con le stesse regole utilizzate per gli orbitali atomici (ad es. un OM può essere occupato solo da 2 elettroni e con spin diversi).

Per ottenere,gli orbitali molecolari con il metodo LCAO si devono osservare le seguenti regole:

1- si possono combinare solo gli orbitali atomici che posseggono energia non troppo diversa tra loro
2- esiste un criterio di massima sovrapposizione e se l’integrale di sovrapposizione è nullo allora anche l’integrale di scambio è nullo. Questo implica che solo gli orbitali più esterni possono venir combinati

3- si possono combinare solo gli orbitali atomici che possiedono la stessa simmetria rispetto all’asse di legame 

ESEMPIO DI CALCOLO PER L’ETILENE

La molecola di etilene H2C=CH2 può essere sinteticamente rappresentata nel modo seguente :

in cui si indica con 1 l’orbitale Pz dell’atomo di C1 e con 2 l’orbitale Pz del C2. Abbiamo pertanto gli orbital Ψ_P1 e Ψ _P2.   (che indicheremo con P1 e P2 )che contribuiscono a formare l’orbitale molecolare Ψ_M.

Possiamo scrivere allora    Ψ_M = a1 P1 + a2 P2

Sostituendo questa funzione nell’equazione di Schrodinger  HΨ = EΨ si ha:

H(a1P1 +a2P2) = E(a1P1+a2P2)   e moltiplicando per ΨM si ha:

(a1P1 +a2P2)H(a1P1 +a2P2) = E(a1P1+a2P2) a1P1 +a2P2)

da cui integrando si ha :  ∫(a1P1 +a2P2)H(a1P1 +a2P2) = E1P1+a2P2) a1P1 +a2P2)

cioè

$E=\frac{\int (a1P1 +a2P2)H(a1P1 +a2P2)}{\int (a1P1 +a2P2)(a1P1 +a2P2)}$

e sviluppando

$E=\frac{a{1}^2\int P1P1 dt +a1a2\int P1P2dt+a2a1\int P2P1 dt +a{2}^2\int P2HP2dt}{a{1}^2\int P1P1 dt +a1a2\int P1P2dt+a2a1\int P2P1 dt +a{2}^2\int p2Hp2dt}$

derivando rispetto ad a ed a1ed a2 ed uguagliando a zero

       δE/δa1 =0  e  δE/δa2 =0

si ha ricordando che la derivata di un quoziente è

              δu/δv =vδu- uδv / v²

$\delta E/\delta a1=0=\frac{(2a1H11 +a2H12+a2H21 +0)(a{1}^{2}S11+a1a2S12+a2a1S21+a{2}^{2}S22)–\left(\right(a{1}^{2}H11+a1a2H12+a2a1H21+a{2}^{2}H22\left)\right(2a1S11+a2S12+a2S21+0)}{(a{1}^{2}S11+a1a2S12+a2a1S21+a{2}^{2}S22) (a{1}^{2}S11+a1a2S12+a2a1S21+a{2}^{2}S22)}$

dove il termine frazionario dopo il segno meno

$\frac{(a{1}^{2 }H11+a1a2H12+a2a1H21+a{2}^{2}H22)}{(a{1}^{2 }S11+q1a2S12+a2a1S21+a{2}^{2 }S22)}= E$

possiamo scrivere:

$\delta E/\delta a1=0=( 2a1H11+a2H12+a2H21) – ( 2a1S11+a2S12+a2S21) E$

(analogo calcolo viene effettuato per a2  )

$\delta E/\delta a1=0= 2 (a1H1– a1S11E) + a2( H12 –S12E) + a2H21( –S21E)$

2a1(H11-S11E) + 2a2(H12-S12E)=0

e dividendo per 2

a1(H11-S11E) + a2(H12-S12E)=0

indicando l’integrale H11=α  e l’integrale H12=H21 =β si ha il determinante

questo determinante è dato da (α-E) (α-E) – β² =0  da cui si ottengono le due radici di E

E1=α+β      ed E2=α-β 

ed essendo β un valore negativo allora E1<E2

I due elettroni π dell’etilene occupano il livello di energia più basso cioè E1  per cui l’energia π della molecola è

E = 2 (α+β)

Se i due elettroni della molecola vengono eccitati, uno di essi occupa il livello di energia E2  per cui l’energia π della molecola diviene

E1= (α+β) + (α-β) = 2α

e l’energia della transizione diviene E2-E1= -2β

CALCOLO DELLA FUNZIONE Ψ CHE CORRISPONDE ALL’ENERGIA E1

Sappiamo che la funzione Ψ ha la seguente forma : Ψ = c11χ1 + c12χ2

ed il sistema associato al determinante è :

c11(α -E1) + c12 β =0

c11β + c12(α -E1)=0

e si riduce ad una sola equazione essendo il determinante corrispondente nullo.

c11(α -E1)  +c12β =0

ma essendo E1= α+β       si ha -c11β +c12β =0

Essendo l’integrale β diverso da zero allora deve essere c11=c12

la funzione cercata ha quindi la forma  Ψ1 = c11(χ1 + χ2)

Il valore di C11 viene calcolato dalla condizione di normalizzazione c11² + c12² =1

essendo c11=c12    allora  C11=C12= ± 1 / √2   pertanto la funzione d’onda corrispondente all’energia E1 della molecola di etilene è  Ψ1 = 1 / √2  (χ1 + χ2).

CALCOLO DELLA CARICA π  NELL’ETILENE

Nello stato fondamentale le cariche elettroniche π sono

q1= 2C11² =1

q2=2C12² =1

nel primo stato eccitato

q1′ = c11² + c12² =1

q2′ = c12² + c22² =1

CALCOLO DEGLI INDICI DI LEGAME

nello stato fondamentale  L12= 2C11 C12 =1

nel primo stato eccitato l’12 =c11c12 +c21c22 =0

   Send article as PDF