TEORIA DEI GRUPPI ED ORBITALI

Consideriamo una molecola con struttura appartenente al gruppo di simmetria D4h, cioè una struttura planare quadrata:

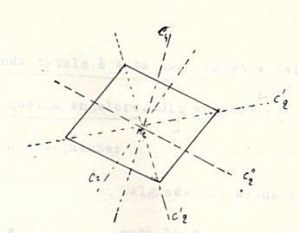 ad esempio PtCl4^-2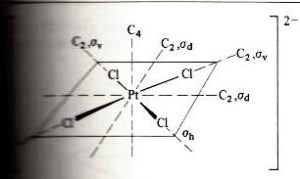 

in cui gli orbitali hanno origine dal centro del quadrato .

Sappiamo che gli orbitali di tipo P per l’ atomo di idrogeno possiedono una parete radiale (che dipende da r ) ed una parte angolare (che dipende dagli angoli degli assi secondo coordinate cartesiane polari cioè gli angoli θ e Φ):

come si vede la parte radiale è identica per i 3 orbitali P mentre varia la parte  angolare.

La funzione d’ onda è il prodotto tra la parte radiale e quella angolare e per atomi con più elettroni le proprietà di simmetria degli orbitali sono analoghe a quelle con un solo elettrone in quanto la parte angolare è uguale mentre la parte radiale differisce solo per le mutue azioni tra gli elettroni, quindi le conclusioni riguardanti la simmetria degli orbitali per un solo elettrone  sono valide anche per atomi polielettronici. Questo significa che per gli atomi polielettronici possiamo usare gli orbitali relativi all’atomo monoelettronico.

Come è noto, queste funzioni sono soluzione dell’equazione di Schrodinger

HΨ =EΨ

dove H è l’ operatore Hamiltoniano che lascia la funzione immutata ma la moltiplica per una costante. Se le funzoni sono Px,Py,Pz avremo

HPx=E1Px

HPy=E2Py

HPz=E3Pz

Siccome i valori E1,E2,E3 sono uguali diciamo che le corrispondenti funzioni Px,Py,Pz sono “DEGENERI”.

Dal momento che sappiamo che effettuare un’operazione di simmetria su una molecola che appartiene ad un determinato gruppo di simmetria significa effettuare un’operazione sull’equazione d’onda che descrive ogni singolo orbitale dell’elemento centrale che lega altri atomi possiamo scrivere

XHPil  = Ei Pil

Questa operazione di simmetria X può lasciare l’ orbitale nella medesima posizione originaria (si indica questo effetto con +1) oppure può modificarne la posizione ( si indica questo effetto con -1).

X Pi = ± 1Pi  cioè

XHPi = HXPi = Ei (± 1Pi)

per gli orbitali degeneri come gli orbitali Px,Py,Pz  non solo è valida la relazione sopra scritta ma è valida anche per una  funzione orbitale nuova formata da una combinazione lineare dei suddetti orbitali (che è sempre soluzione dell’equazione di Schrodinger ) cioè:

Pil= a1Px+a2Py+a3Pz 

dove a1,a2,a3 indicano la quantità di orbitale Px,Py e Pz che partecipa alla combinazione, quindi

XHPil = HXPil in cui XH =HX per cui si dice che gli operatori X ed H “commutano”.

XHPil = HXPil = EiPil

ed anche  XPil= ∑³ _j=1   xij Pij

Se effettuiamo una nuova operazione di simmetria B avremo

BPij  = ∑³ _m=1  bmij Pim

se effettuiamo prima l’operazione X e poi quella B avremo un’ operazione C che appartiene allo stesso gruppo di X e B

BXPil= CPil

CPil = B ∑³ _j=1   xij Pij = ∑³ _j=1 ∑³ _m=1  bmj Xjl Pim

C_ml =  ∑³_j=1 b_mj X_ij

La relazione sopra scritta non è altro che l’espressione analitica degli elementi di una matrice prodotto per cui se sottoponiamo le funzioni date ad operazioni di simmetria queste danno origine ad un gruppo. Vediamo adesso quali sono le matrici di trasformazione degli orbitali p.

La forma degli orbitali p in un complesso planare quadrato è

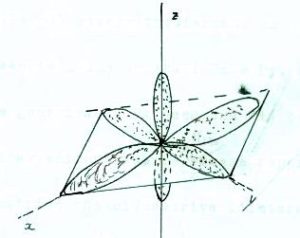
Agendo su questi orbitali con operazioni di simmetria D4h (poichè stiamo trattando una molecola planare quadrata ) avremo

1 ) l’orbitale può coincidere con la posizione da esso occupata prima dell’operazione (+1)

2) l’ orbitale può occupare una posizione diversa dall’originaria e può coincidere con un orbitale diverso. Ciò significa che per esempio se  Px dopo l’operazione X occuoerà la posizione di Py si avrà la matrice :

$\left|\begin{array}{cc}\int PxXPx dt& \int PxXPy dt\\ \int PxXPx dt & \int PyXpy dt\end{array}\right|$

In generale un orbitale si trasforma in altri due orbitali al massimo e ciò accade con le molecole a simmetria ottaedrica o tetraedrica (O_h e T_d)

L’operazione identità del gruppo D4h lascia immutati i due orbitali Px e Py

EPx = +1 Px

EPy= +1 Py

in forma di matrice possiamo scrivere

$\left|\begin{array}{cc}1& 0\\ 0& 1\end{array}\right|\left|\begin{array}{c}Px\\ Py\end{array}\right|$

La matrice di trasformazione ha quindi un carattere dato da χ = 1 +1 =2    χ_E=2

L’operazione C2 (rotazione intorno ad un asse C2) sposta i 2 orbitali verso la parte negativa degli assi quindi:

C2 Px= -1 Px

C2 Py = -1 Py       in forma di matrice  :

$\left|\begin{array}{cc}–1& 0\\ 0& –1\end{array}\right|\left[\begin{array}{c}Px\\ Py\end{array}\right]= \left|\begin{array}{cc}–Px& 0\\ 0& –Py\end{array}\right|$

il carattere della matrice di trasformazione C2 = χ=-1 + -1 = -2       χ _C2=-2

Delle due  operazioni C’2 , la prima cambia di segno Px ma lascia immutato Py

C’2 Px= -Px

C’2 Py = Py  cioè

$\left|\begin{array}{cc}–1& 0\\ 0& +1\end{array}\right|\left[\begin{array}{c}Px\\ Py\end{array}\right]=\left|\begin{array}{cc}–Px& 0\\ 0& +Py\end{array}\right|$

il cui carattere è   χ _C’2=0

Le operazioni C”2 cambiano di segno Px che diventa -Py    e Py che diviene – Px cioè

C”2 Px = -Py

C”2 Py = -Px

questo tipo di interazione è rappresentato dalla matrice seguente:

$\left|\begin{array}{cc}\int Px{C}_2^{“}Px dt & \int Px{C}_2^{“}Py dt \\ \int Py{C}_2^{“}Px dt & \int Py{C}_2^{“}Py dt \end{array}\right|$

il primo termine

$$\begin{gathered} \int Px{C}_2^{“}Px dt = \int Px(–Py) dt in quanto C_2^{“}Px = –Py inoltre \\ essendo \int \psi a\psi b dt =0 allora il valore di \int Px(–Py) dt =0 \end{gathered}$$

Il secondo integrale ∫ -PxPxdt = -1  in quanto sappiamo che ∫ψaψb dt =1 . In definitiva il carattere della trasformazione C2″ è :

$\left|\begin{array}{cc}0& –1\\ –1& 0\end{array}\right|$

il cui carattere è χ = 0

seguendo analogo ragionamento per tutte le operazioni del gruppo D4h si hanno i seguenti caratteri :

  D4h              E    2C4   C2  2C’2   2C”2    i    2S4   σ_h     2 σ _v     2 σ_d

Px , Py            2     0      -2     0         0       -2     0      2      0             0

per lìorbitale Pz  invece si ha

  D4h              E    2C4   C2  2C’2   2C”2    i    2S4   σ_h     2 σ _v     2 σ_d

pz                1      1       1     -1         -1        -1    -1     -1          1           1

abbiamo così trovato le cosiddette “rappresentazioni riducibili” degli orbitali Px,Py,Pz.

Con lo stesso procedimento operiamo sugli orbitali d la cui espressione analitica è :

e la loro forma è

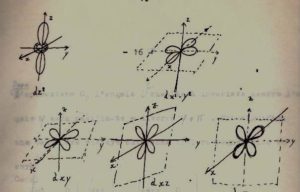
se consideriamo gli orbitali dxz  e dyz otteniamo per l’operazione E che gli angoli θ e  φ non vengono modificati quindi le funzioni rimangono inalterate ed in termini di matrice :

$\left|\begin{array}{cc}1& 0\\ 0& 1\end{array}\right|\left[\begin{array}{c}dxz\\ dyz\end{array}\right]= \left|\begin{array}{cc}+1dxz& 0\\ 0& +1dyz\end{array}\right| per cui {\chi }_E =2$

seguendo analogo procedimento troviamo che C2 lascia inalterato θ ma varia φ che diviene  φ + π il che significa che tanto dxz che dyz variano di segno e quindi

$\left|\begin{array}{cc}–1& 0\\ 0& –1\end{array}\right|\left[\begin{array}{c}dxz\\ dyz\end{array}\right]=\left|\begin{array}{cc}–dxz& 0\\ 0& –dyz\end{array}\right| e {\chi }_{c2} = –2$

l’operazione C2′ trasforma l’angolo θ in π – θ e l’angolo φ in – φ per cui l’orbitale dxz non viene modificato mentre si cambia di segno l’orbitale dyz

$\left|\begin{array}{cc}1& 0\\ 0& –1\end{array}\right|\left[\begin{array}{c}dxz\\ dyz\end{array}\right]= \left|\begin{array}{cc}+dxz& 0\\ 0& .dyz\end{array}\right| per cui {\chi }_{C‘2}^{}= 0$

seguendo sempre questo procedimento per tutti gli orbitali osserviamo la seguente tavola dei caratteri riducibili

D4h           E   2C4     C2   2C’2  2C”2    i  2S4   σh    σv     σd

dxz,dyz      2    0        -2       0      0        2    0     -2      0       0

dz²              1    1          1        1       1        1     1       1      1         1

dz²-y²        1  – 1          1      -1      -1        1   -1       1     -1       -1

dxy             1   -1          1      -1        1        1   -1       1     -1        1

se osserviamo la rappresentazione del gruppo D4h vediamo che dz² si trasforma come A1g , dx²-y² si trasforma come B1g, dxy come B2g, dxz e dyz come Eg mentre pz come A2u e Px,py come Eu.

Come è possibile notare, le Rappresentazioni irriducibili del gruppo sono state indicate con gli indici G ed u (gerade ed ungerade) che significano nel caso di g che la rappresentazione è simmetrica rispetto all’inversione ed nel caso di u è non simmetrica.Inoltre la lettera A indica rappresaentazioni di dimensione 1 e B invece di dimensione 2.

Ovviamente, il procedimento è valido per molecole con struttura ottaedrica o tetraedrica ma essendo piuttosto elaborato, useremo un metodo più semplice per ottenere i caratteri delle rappresentazioni Riducibili che poi ridurremo a quelle irriducibili semplicemente considerando quali orbitali rimangono in posizione invariata dopo l’operazione di simmetria.

   Send article as PDF